Physics Question - Printable Version
-Shoutbox (https://shoutbox.menthix.net)
+-- Forum: MsgHelp Archive (/forumdisplay.php?fid=58)
+--- Forum: General (/forumdisplay.php?fid=11)
+---- Forum: General Chit Chat (/forumdisplay.php?fid=14)
+----- Thread: Physics Question (/showthread.php?tid=93951)
Physics Question by prashker on 02-24-2010 at 08:42 PM
![[Image: physics_16471.png]](http://sonicsam.net/files/dump/physics_16471.png)
THIS IS NOT TO SCALE.
The only information I know is
Left Side = Longer Chain/Flatter Slope
Right Side = Shorter Chain/Steeper Slope
This is a thought experiment, hence the frictionless surface and no numbers.
Am I right? If not, explain possible outcomes 
RE: Physics Question by Chrissy on 02-24-2010 at 08:55 PM
I think, right side.
Steeper slope = more gravity pull and since there is no friction the rest of the chain will just flow as well.
RE: Physics Question by Joa on 02-24-2010 at 09:04 PM
left because of the mass (like you said)
krissy the gravity pull affects both sides.. on the left there is more chain (and since there is no friction i'd assume the chain will slide the way where it's weight is greatest)
RE: Physics Question by prashker on 02-24-2010 at 09:06 PM
krissy's is what I originally thought, however the way you said Joa seems to make more sense
RE: Physics Question by MeEtc on 02-24-2010 at 09:14 PM
It depends not on the mass of each side, but the force of gravity exerting on the ramp in a vertical direction. The above example is indeterminate without the angles of the slope and length of chain on each side. Assuming the mass of the chain is evenly distributed, the mass itself irreverent, just the length of the chain is needed.
RE: Physics Question by Chrissy on 02-24-2010 at 09:15 PM
The gravity will effect the right hand side more though
RE: Physics Question by MeEtc on 02-24-2010 at 09:22 PM
quote:True, but there is more chain on the left side. As I said, the question is indeterminate without actual data
Originally posted by krissy-afc
The gravity will effect the right hand side more though
RE: RE: Physics Question by Joa on 02-24-2010 at 09:23 PM
quote:
Originally posted by MeEtc
It depends not on the mass of each side, but the force of gravity exerting on the ramp in a vertical direction. The above example is indeterminate without the angles of the slope and length of chain on each side. Assuming the mass of the chain is evenly distributed, the mass itself irreverent, just the length of the chain is needed.
so theoretically without all the exact info - right now one could even say that the chain could remain in place because perhaps the pull of gravity is evenly distributed on both sides due to the angle and length of chain
![[Image: mmm.gif]](http://shoutbox.menthix.net/images/smilies/zippy/mmm.gif)
...edit : i cba to reword what i said
... i know it's not worded correctly at all 
- just get the gist of my general idea
RE: Physics Question by djdannyp on 02-24-2010 at 09:23 PM
quote:
Originally posted by krissy-afc
The gravity will effect the right hand side more though
Not true is it?
Physics isn't my strong point, but it was said on QI that a bullet being fired while aimed parallel to the ground at arm's length will hit the ground at the same time as if you simply drop a bullet held at the same height. Showing that gravity acts the same on objects regardless of the force/direction
Doesn't the same thing kinda apply here to disprove that?
RE: Physics Question by vaccination on 02-24-2010 at 10:12 PM
Gravity's effect on the chain will be the same, no matter the slope, what you have to take into account is the mass on each side of the pivot point [in this case the point where the two slopes meet], assuming the chain is uniform across it's entire length, the side with the most mass is the side with the longest part of chain [the left side]. Due to F = mgh, the force acting on the side with the most mass will be greatest [since in this example height and gravity can be considered constants], therefore the chain should fall off the left side.
Of course, I've not taken into account the vertical component force of the slope acting against gravity, but in a frictionless experiment, I would tend to imagine this wouldn't matter...as much. =p
Then again, I much prefer physics with numbers than theoretical physics.
Also, I agree that without any ballpark figures, there are multiple outcomes, if the flat slope is only sloping at a small angle the slope would become negligible and the chain would likely fall right, similarly if the angles are just right, they would balance. My above theory goes from a setup like the one in Sam's pic, where the left (flat) slope is at a considerable angle, and the right slope is almost irrelevant to the shorter chain.
quote:
No, simply because the in the QI version the force [air resistance as the bullet falls vertically] acting against gravity is the same, in this experiment, the force acting against gravity is different for the two sides of chain.
Originally posted by djdannyp
Physics isn't my strong point, but it was said on QI that a bullet being fired while aimed parallel to the ground at arm's length will hit the ground at the same time as if you simply drop a bullet held at the same height. Showing that gravity acts the same on objects regardless of the force/direction
Doesn't the same thing kinda apply here to disprove that?
---
quote:
Originally posted by MeEtc
It depends not on the mass of each side, but the force of gravity exerting on the ramp in a vertical direction. The above example is indeterminate without the angles of the slope and length of chain on each side. Assuming the mass of the chain is evenly distributed, the mass itself irreverent, just the length of the chain is needed.
The mass isn't evenly distributed about the pivot though, else the problem wouldn't occur and the chain wouldn't fall either way. Assuming a uniform chain, the longer side will have more mass, thus it's weight will be greater.
RE: Physics Question by foaly on 02-24-2010 at 11:25 PM
Ok it's way late so I might be dead wrong.
But since there is a possible balance, shouldn't you take the distance from the thumble point into account?
So you would get:
If the chain is as longer on the left as it is less steep, there will be a balance, and if it is either longer or steeper it will fall an the left, shorter or less steep on the right...
RE: Physics Question by Spunky on 02-24-2010 at 11:55 PM
From my experiences of balancing chains on corners of tables (
), I think it would balance out, but I suppose it does depend on the exact values
RE: Physics Question by blessedguy on 02-25-2010 at 12:09 AM
![[Image: c938fa0908811e439b481e9747eb06f7.png]](http://grab.by/grabs/c938fa0908811e439b481e9747eb06f7.png)
A (alpha) and G (gamma) are shown above. AB is some line that crosses both AC and BC, and DC crosses BA perpendiculary and is in the same direction as the gravitional camp, which by convention points downside.
The chain will fall on the side of bigger cos*mass product:
if (cos A)*(mass of chain above BC) > (cos G)*(mass of chain above AC), it will fall to the left.
if (cos A)*(mass of chain above BC) < (cos G)*(mass of chain above AC), to the right.
Or I need to revise it again =P.
P.S.: Codification: making non-latin symbols fail to renderize since the beggining.
Other P.S.: Swithced the sides after correcting it 
RE: Physics Question by prashker on 02-25-2010 at 12:21 AM
I believe I can conclude that it'll fall to the left .
My teacher basically gave me this problem and said "ask anyone".
On the picture provided in class, it specifically said it could be done without calculating "and all that blah blah"
RE: Physics Question by Chrono on 02-25-2010 at 12:22 AM
i think
quote:
Originally posted by blessedguy
A (alpha) and G (gamma) are shown above. AB is some line that crosses both AC and BC, and DC crosses BA perpendiculary and is in the same direction as the gravitional camp, which by convention points downside.
The chain will fall on the side of bigger cos*mass product:
if (cos A)*(mass of chain above BC) > (cos G)*(mass of chain above AC), it will fall to the left.
if (cos A)*(mass of chain above BC) < (cos G)*(mass of chain above AC), to the right.
Or I need to revise it again =P.
P.S.: Codification: making non-latin symbols fail to renderize since the beggining.
* Chrono agrees
RE: RE: Physics Question by Veggie on 02-25-2010 at 10:26 AM
quote:yeah that looks right, if not i didnt learn anything from my engineering degree
Originally posted by Chrono
i thinkquote:
Originally posted by blessedguy
A (alpha) and G (gamma) are shown above. AB is some line that crosses both AC and BC, and DC crosses BA perpendiculary and is in the same direction as the gravitional camp, which by convention points downside.
The chain will fall on the side of bigger cos*mass product:
if (cos A)*(mass of chain above AC) > (cos G)*(mass of chain above BC), it will fall to the left.
if (cos A)*(mass of chain above AC) < (cos G)*(mass of chain above BC), to the right.
Or I need to revise it again =P.
P.S.: Codification: making non-latin symbols fail to renderize since the beggining.
* Chrono agrees
RE: Physics Question by gif83 on 02-25-2010 at 07:12 PM
quote:
Originally posted by blessedguy
A (alpha) and G (gamma) are shown above. AB is some line that crosses both AC and BC, and DC crosses BA perpendiculary and is in the same direction as the gravitional camp, which by convention points downside.
The chain will fall on the side of bigger cos*mass product:
if (cos A)*(mass of chain above BC) > (cos G)*(mass of chain above AC), it will fall to the left.
if (cos A)*(mass of chain above BC) < (cos G)*(mass of chain above AC), to the right.
Or I need to revise it again =P.
P.S.: Codification: making non-latin symbols fail to renderize since the beggining.
Other P.S.: Swithced the sides after correcting it
Erm, if mass of chain is uniformly distributed, shouldn't the equations balance?
Mass being proportional to the hypotenuse of each side DC/cos(alpha) and DC/cos(gamma) respectively...
RE: Physics Question by Chancer on 02-26-2010 at 01:28 AM
You can think of 2 blocks instead of a chain. It's the same thing:
W, W' = blocks' weights
T = tension in the rope
RE: Physics Question by Volv on 02-27-2010 at 12:25 AM
quote:This (as well as Chancer's) is 100% correct. Given that, I think Joa's probably got the answer your teacher is looking for with:
Originally posted by blessedguy
if (cos A)*(mass of chain above BC) > (cos G)*(mass of chain above AC), it will fall to the left.
if (cos A)*(mass of chain above BC) < (cos G)*(mass of chain above AC), to the right.
quote:This is because cos
Originally posted by Joa
so theoretically without all the exact info - right now one could even say that the chain could remain in place because perhaps the pull of gravity is evenly distributed on both sides due to the angle and length of chain
is a smaller value but BC is greater in mass whereas cos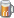
is a greater value but AC is of smaller mass, essentially cancelling out one another for no net movement. The only reason I think your teacher would have asked this question in such vague terms would be if that was the answer she was looking for even though technically that can't be concluded without assigning values to the lengths of the chain and angles.
RE: Physics Question by prashker on 02-27-2010 at 12:31 AM
quote:Heh, we'll find out soon when (and if) he tells us
Originally posted by Volv
The only reason I think your teacher would have asked this question in such vague terms would be if that was the answer she was looking for even though technically that can't be concluded without the mass of the chain or angles assigned values.
RE: Physics Question by toddy on 02-27-2010 at 12:40 AM
doesn't move
RE: RE: Physics Question by CookieRevised on 02-27-2010 at 05:02 AM
quote:no it wont...
Originally posted by krissy-afc
The gravity will effect the right hand side more though
The angles are irrelevant in a _frictionless_ environment**...
And since you don't have friction, you also do not need to know the exact figures like mass, angles, length, etc. All you need to know is that one end is longer than the other and that they are both slopes. So, the question isn't actual 'vague' at all.
** Unless the angle would be 0° (flat), in that case the gravitational pull on the left is cancelled out by the counterforce of the flat bed. And since there is nothing to 'hold' the chain on the right (it isn't flat; thus no counterforce), it would move right... very very slowly at first of course, but it will move...
*assuming the total mass of the chain is evenly distributed across its length of course.
PS: A chain isn't going to fall slower if you hold it in a 45° angle than when you hold it in a 90° angle! It would fall just as quick in a frictionless environment.
Or put in another way, if there is no friction, the angle of the slopes don't matter and could also be both 90° for all it matters. Looking it that way I think there would be no doubt that the chain would fall to the left.
This is exactly the same question as what would fall faster in a vacuum: 10Kg feathers or 10Kg lead. The answer is, because there is no friction (air resistance) to take in account: they fall at the same speed. In the real world 10Kg feathers would fall slower because of the air resistance/friction.
*at least I think, no?*
EDIT: no
RE: Physics Question by Volv on 02-27-2010 at 05:16 AM
Frictionless just means there's no counterforce along (i.e. preventing it from sliding across the surface), both Chancer and blessedguy already incorporated that into their models.
Regardless of friction, a component of the gravitational force on the object is into the sloping surface and similarly the ground is exerting an equal force onto the object at an angle perpendicular to the surface (see Wcos in Chancer's model) which acts to cancel out a part of the gravitational force.
Probably a bit more intuitive to think of a practical example:
A man who is skating across ice which is angled ever so slightly downwards will not be accelerating at anywhere even remotely near the same rate at which a man who fell through the ice (or jumped out of a plane) would be.
The only difference friction would make is that there would be an additional force acting in the same direction as T (the tension on the rope in Chancer's model) i.e. across the surface, preventing it from sliding -- which as you can see has been omitted in his model 
PS: I know im terrible at explaining stuff
One last go: a portion of the gravitational force is into the surface which is completely counteracted by equal+opposite force (stopping it from falling through the object). Therefore the only remaining net force is that portion of the gravitational force which remains.
The lesser the slope, the greater the component of the gravitational force which is counteracted (as there is a greater portion being applied into the surface).
RE: Physics Question by Felu on 02-27-2010 at 06:52 AM
quote:What has mass got to do with acceleration due to gravity? In a vacuum, even 1g of feather would fall in the same time as 10kg of lead, if dropped from the same height.
Originally posted by CookieRevised
This is exactly the same question as what would fall faster in a vacuum: 10Kg feathers or 10Kg lead. The answer is, because there is no friction (air resistance) to take in account: they fall at the same speed. In the real world 10Kg feathers would fall slower because of the air resistance/friction.
RE: Physics Question by gif83 on 02-27-2010 at 06:58 AM
I think what Volv is trying to explain here is that the force of gravity has been restricted to that of the motion of the plane due to the slope being an immovable plane.
So when we measure Force along (parallel to) the plane, it becomes a component of the downwards force.
This is described in blessedguy's post as proportional to (cos A)*(mass of chain above BC) or Chancer's post as W sin ( a ).
(On the left hand side)
Both being the same thing really.
My previous post was showing the proportions of mass on either side as being proportional to the inverse of these values.
This shows no movement in the chain.
Been a while since I've done maths. Good brain exercise.
RE: Physics Question by CookieRevised on 02-27-2010 at 07:13 AM
quote:yes, but they are made the same weight exactly to rule out the difference in weight; to keep things simple when you do the 'experiment' in a non-vacuum environment.
Originally posted by Felu
quote:What has mass got to do with acceleration due to gravity? In a vacuum, even 1g of feather would fall in the same time as 10kg of lead, if dropped from the same height.
Originally posted by CookieRevised
This is exactly the same question as what would fall faster in a vacuum: 10Kg feathers or 10Kg lead. The answer is, because there is no friction (air resistance) to take in account: they fall at the same speed. In the real world 10Kg feathers would fall slower because of the air resistance/friction.
--------------
Volv, reading your example made me see the error, thanks. (wasn't such a crappy example as you thought afterall
). So I stand corrected...-
But I now think, and even convinced, that the chain wouldn't move at all actually, no matter what the angles are (so even no math or equations needed)
The whole thing is like a static block.Think about it, what if you have something hanging from below connecting both ends of the chain. It would mean that there would be a 'force' pulling on each side eaqually from below no (so it doesn't matter if it is there or not)? So, if the top piece of the chain would move to some direction, it means the bottom part would move too (in the opposite direction). If that would happen, you would have something like a perpetual machine! Which isn't possible becaue there is no force to maintain it... hence, it would never move, no matter the angles and the lengths of the slopes, as long as both the 'bottom' parts are on a horizontal plane. Or am I missing something again (quite possible though, I'm not that awake anymore)?...
EDIT: wait... ermmm.
EDIT2: yeah, no movement...
EDIT3: ermm... hang on ... blah.... I give up... and now I can't sleep thinking about this all morning (8am already)
* CookieRevised shoots SonicSam for asking such questions...
RE: Physics Question by toddy on 02-27-2010 at 07:28 AM
quote:how would it be a perpetual machine
Originally posted by CookieRevised
If that would happen, you would have a perpetual machine! Which isn't possible
RE: Physics Question by CookieRevised on 02-27-2010 at 07:33 AM
quote:because if it would move, it would keep on moving forever because nothing has changed in the system compared to the previous move because one end was connected to the other end. So, let's say it moves to the left (counterclockwise) on top, then a piece of the bottom chain would move a bit up to the right and a new piece from the once on top chain would become now the bottom chain. Again having equally amount of 'chain' on the top. Because it is the same length, mass, whatever as before. So the system is still the same. And hence, if it would have moved the first time it should be moving again now, (EDIT) like a perpetual machine. But that isn't possible.
Originally posted by toddy
quote:how would it be a perpetual machine
Originally posted by CookieRevised
If that would happen, you would have a perpetual machine! Which isn't possible
EDIT: I meant: it is _like_ a perpetual motion machine _if_ the first inital movement made sense and if there is something to maintain it (aka if there was some unbalance in forces).
I really should not post when I'm tired, sorry
RE: Physics Question by gif83 on 02-27-2010 at 07:34 AM
quote:
Originally posted by CookieRevised
quote:yes, but they are made the same weight exactly to rule out the difference in weight; to keep things simple when you do the 'experiment' in a non-vacuum environment.
Originally posted by Felu
quote:What has mass got to do with acceleration due to gravity? In a vacuum, even 1g of feather would fall in the same time as 10kg of lead, if dropped from the same height.
Originally posted by CookieRevised
This is exactly the same question as what would fall faster in a vacuum: 10Kg feathers or 10Kg lead. The answer is, because there is no friction (air resistance) to take in account: they fall at the same speed. In the real world 10Kg feathers would fall slower because of the air resistance/friction.
--------------
Volv, reading your example made me see the error, thanks. (wasn't such a crappy example as you thought afterall
-
But I now think, and even convinced, that the chain wouldn't move at all actually, no matter what the angles are (so even no math needed)
Think about it, what if you have something hanging from below connecting both ends of the chain. It would mean that there would be a 'force' pulling on each side eaqually from below no (so it doesn't matter if it is there or not)? So, if the top piece of the chain would move to some direction, it means the bottom part would move too (in the opposite direction). If that would happen, you would have a perpetual machine! Which isn't possible... hence, it would never move, no matter the angles and the lengths of the slopes, as long as both the 'bottom' parts are on a horizontal plane. Or am I missing something again (quite possible though, I'm not that awake anymore)?...
EDIT: wait... ermmm.
EDIT2: yeah, no movement...
EDIT3: ermm... hang on ... blah.... I give up... and now I can't sleep thinking about this all morning (8am already)
* CookieRevised shoots SonicSam for asking such questions...
hahaha why are you connecting the chain at the bottom?
Get some sleep cookie. You really need it.
RE: Physics Question by CookieRevised on 02-27-2010 at 07:36 AM
quote:dunno, why not.... does that matter that you connect it? it doesn't add or substract any more 'force' on one side compared to the other side, does it?
Originally posted by gif83
hahaha why are you connecting the chain at the bottom?
As long as both the 'ends' in SonicSam's drawing are meant to be at equal height (on the same horizontal plane) though...
quote:will do ... or at least try...
Originally posted by gif83
Get some sleep cookie. You really need it.
RE: Physics Question by Rolando on 02-27-2010 at 07:41 AM
You guys are looking too into it.. this ins't a college problem. It's a simple physics problem.
RE: Physics Question by gif83 on 02-27-2010 at 07:48 AM
quote:
Originally posted by CookieRevised
dunno, why not.... does that matter that you connect it? it doesn't add or substract any more 'force' on one side compared to the other side, does it?
Well yeah it does, in fact it changes the whole system.
Think about it after a sleep.
Close your eyes and count SonicSams
P.S. perpetual motion is possible in theoretical physics where such things as frictionless planes exist.
RE: Physics Question by CookieRevised on 02-27-2010 at 07:58 AM
How does it change the system? You simply add like 10kg to one end and 10kg to the other so to speak... you simply add the same pulling force to both ends, so it would be as if it would never be there as it would cancel out anyways in those equations. It's like saying x/y wouldn't be the same as x+10 / y+10.... (x and y being those formulas or whatever you have in above posts). And come to think of it, that even goes no matter if there is friction or not!
Or take both ends of such a chain in your hands and let yourself hang... you aren't going to move all of sudden, the chain isn't going to pull you up on one side; you would hang there motionless (assuming you would weight the same or less than the chain).
quote:yeah, but friction or not, the chain wouldn't move, even in theory. I think the frictionless thingie is just to throw you off or something...
Originally posted by gif83
P.S. perpetual motion is possible in theoretical physics where such things as frictionless planes exist.
blah... going to sleep now before I change my mind again
quote:aaaaaarrgggghh noooooooo
Originally posted by gif83
Close your eyes and count SonicSams
EDIT: I just thought of another way of seeing it and prove why it wouldn't move (you get that when you're counting SonicSams
): look at the two limits of the system. In the first limit example, the two planes have an infinite small angle (aka flat): the chain wouldn't move, no matter how long one end is, and friction or not. In the other limit example, the two planes are both 90°, which means both ends of the chain simple hang strait down from a point right in the middle of the chain, again, no movement, no matter if there is friction or not.... back to counting SonicSams now...
RE: Physics Question by Volv on 02-27-2010 at 08:56 AM
With no friction a wheel would continue turning in a vacuum indefinitely (even though there's gravity). A chain (or rather a smooth string with no ridges) on a spindle would do the same in the same conditions. Unintuitive things happen when you eliminate fundamental principles of physics, doesn't necessarily make the model useless, just limited.
RE: Physics Question by vaccination on 02-27-2010 at 09:29 AM
Lol cookie, perpetual motion is possible in a frictionless environment, the problem is in real life there isn't such a thing Though, supercooled materials are pretty interesting in that area. (plus, there are many other factors which make perpetual motion inconceivable)
RE: Physics Question by CookieRevised on 02-27-2010 at 09:51 AM
quote:But only if there is a force which starts the motion though, and that's only to begin with. With the chain system depicted above, there isn't such an 'starting' force.
Originally posted by Volv
With no friction a wheel would continue turning in a vacuum indefinitely (even though there's gravity).
quote:Perpetual motion machines aren't possible, not even in theory, not even in a frictionless environment since there should always be an equilibrium of energy. And a perpetual motion machine is exactly based on the nonequilibrium of energy (being it motion energy, heat energy or whatever energy): it produces more energy than you put into it, that's the whole definition of such machines.
Originally posted by vaccination
Lol cookie, perpetual motion is possible in a frictionless environment,
The fact that it is said that a perpetual motion machine is not possible in practice is not _just_ because of friction, but mostly because you can not get more energy out of something than you put into it (while preserving its mass). friction is only a tiny part of the problem of perpetual motion machines. Cancelling that out and you would still have the same problems as before: you can not get more energy out of it than you have put into it.
So, forgetting the fact that it isn't possible to completely rule out friction (even with supercooled, superconductors or whatever), thus in a theoretical friction free world, the moment you want to extract energy out of such a perpetual motion machine means that you will eventually loose the stored energy in that machine. And therefore it isn't a real perpetual motion machine to begin with as it will eventually run out.
-
There is no more (or less) force pulling on the chain on the left side than there is on the right side, ergo, there is nothing to start movement, ergo there is no movement, even in a theoretical frictionless system, no matter what angle or length the two slopes are, as long as both ends are on the same horizontal plane. The system is always in equilibrium.
I'm (almost) sure that if you take those equations from above and work them further out you would see they are equal (you can in theory because there is always a direct relation between the various elements of the two sides (mass, length, angle, etc), by using ratios instead of real numbers)). The more I think about it the more I am convinced of that.
RE: Physics Question by Volv on 02-27-2010 at 10:16 AM
I've got a practical experiment for you to try out.
1) Put a long (30cm for example) thin chain (the smaller the links the better) on a very steep ramp which it can slide down easily and watch it slide down.
2) Repeat, this time placing 5mm of the chain over the top of the ramp, observe and record results.
3) Repeat with 1cm over the top of the ramp.
RE: Physics Question by CookieRevised on 02-27-2010 at 10:26 AM
quote:That practice example is not the same as the system above (if you always keep the same angle of the ramps)! Both the ends of the chain must be at the same horizontal plane, see picture from SonicSam.
Originally posted by Volv
I've got a practical experiment for you to try out.
1) Put a long (30cm for example) thin chain (the smaller the links the better) on a very steep ramp which it can slide down easily and watch it slide down.
2) Repeat, this time placing 5mm of the chain over the top of the ramp, observe and record results.
3) Repeat with 1cm over the top of the ramp.
Which means that in your step 2 the long ramp would be almost flat.
In your step 3, the long ramp would be slightly steeper than in step 2. Etc...
Doing that, at any time, the chain will not move at all.
Similar: in your step 1: the long ramp would be completely flat. Again the chain will (in this case obviously) not move. See my previous post where I explained the limits of the system.
-------------
EDIT: a pic to make my ramblings a bit more clear (also for myself
)... can't sleep anyways... note: I suck at drawing a sloped chain with just a laptop mousepad...The first three are very obvious (limit) cases of SonicSam's picture. In those three cases it is very obvious that there is no movement:
1) Extreme limit case, planes are both flat.
2) 'Center' case, both planes are of equal length and thus equally steep
3) Other extreme limit case, planes are both at 90°
4) SonicSam's picture.
The green line is what I talked about in this post:
You simply hang a second chain of the same type as the one you had on both the ends. This does _not_ change anything in the system since the chain would pull equally hard on both sides; aka the two opposite forces (one on the left end, the other on the right end) cancel eachother out. But, it is now a lot easier to see in pic4 why there wouldn't be a movement, not even in a frictionless environment; it's just a closed chain hanging on a irregular object; it is never going to move out of itself.
Or to put it in another way: say that it does move counterclockwise by some freak thing in nature. That would mean that part of the green part of the chain is now on the right slope and part of the red left-sloped chain is now hanging from the left slope below it. In that case there hasn't actually been any change in mass or whatever in any point of the system; we would still have the same amount of chain hanging below and the same amount of chain hanging over the triangle. So why would it have moved the first time if there wasn't any change to begin with? It wouldn't.
Or, by definition and in the opposite way: if it did move by that freak thing in nature, it would keep on moving because after the initial move the system is again exactly the same as before the move. Aka if it moved a first time, it should also move a second time, and a third time, etc, untill infinity. (= what I meant to say to toddy here).
RE: Physics Question by Volv on 02-27-2010 at 10:34 AM
If that was a parameter of SonicSam's question then yes, you are absolutely right
RE: Physics Question by foaly on 02-27-2010 at 01:21 PM
quote:
Originally posted by CookieRevised
You simply hang a second chain of the same type as the one you had on both the ends. This does _not_ change anything in the system since the chain would pull equally hard on both sides; aka the two opposite forces (one on the left end, the other on the right end) cancel eachother out. But, it is now a lot easier to see in pic4 why there wouldn't be a movement, not even in a frictionless environment; it's just a closed chain hanging on a irregular object; it is never going to move out of itself.
It would actually, you move the centerpoint of the mass of the chain...
RE: Physics Question by Chrono on 02-27-2010 at 01:29 PM
quote:1/2 != 11/12
Originally posted by CookieRevised
It's like saying x/y wouldn't be the same as x+10 / y+10.
RE: Physics Question by vaccination on 02-27-2010 at 02:20 PM
quote:
Originally posted by CookieRevised
quote:Perpetual motion machines aren't possible, not even in theory, not even in a frictionless environment since there should always be an equilibrium of energy. And a perpetual motion machine is exactly based on the nonequilibrium of energy (being it motion energy, heat energy or whatever energy): it produces more energy than you put into it, that's the whole definition of such machines.
Originally posted by vaccination
Lol cookie, perpetual motion is possible in a frictionless environment,
The fact that it is said that a perpetual motion machine is not possible in practice is not _just_ because of friction, but mostly because you can not get more energy out of something than you put into it (while preserving its mass). friction is only a tiny part of the problem of perpetual motion machines. Cancelling that out and you would still have the same problems as before: you can not get more energy out of it than you have put into it.
So, forgetting the fact that it isn't possible to completely rule out friction (even with supercooled, superconductors or whatever), thus in a theoretical friction free world, the moment you want to extract energy out of such a perpetual motion machine means that you will eventually loose the stored energy in that machine. And therefore it isn't a real perpetual motion machine to begin with as it will eventually run out.
Why ignore half my post? -.-
quote:
Originally posted by CookieRevised
There is no more (or less) force pulling on the chain on the left side than there is on the right side, ergo, there is nothing to start movement, ergo there is no movement, even in a theoretical frictionless system, no matter what angle or length the two slopes are, as long as both ends are on the same horizontal plane. The system is always in equilibrium.
I'm (almost) sure that if you take those equations from above and work them further out you would see they are equal (you can in theory because there is always a direct relation between the various elements of the two sides (mass, length, angle, etc), by using ratios instead of real numbers)). The more I think about it the more I am convinced of that.
Uhm, yes there is. F = mgh. The force due to gravity is greater on the left side as there is more mass.
quote:
Originally posted by foaly
quote:
Originally posted by CookieRevised
You simply hang a second chain of the same type as the one you had on both the ends. This does _not_ change anything in the system since the chain would pull equally hard on both sides; aka the two opposite forces (one on the left end, the other on the right end) cancel eachother out. But, it is now a lot easier to see in pic4 why there wouldn't be a movement, not even in a frictionless environment; it's just a closed chain hanging on a irregular object; it is never going to move out of itself.
It would actually, you move the centerpoint of the mass of the chain...
I was just about to point this out, connecting the ends of the chain like you have in the image COMPLETELY changes to whole system and cannot be considered.
RE: Physics Question by gif83 on 02-27-2010 at 06:52 PM
quote:
Originally posted by CookieRevised
I'm (almost) sure that if you take those equations from above and work them further out you would see they are equal (you can in theory because there is always a direct relation between the various elements of the two sides (mass, length, angle, etc), by using ratios instead of real numbers)). The more I think about it the more I am convinced of that.
I already showed this in both my posts. Maybe it's hard for you to understand that without diagrams. The equations do equate.
I'm still not entirely sure how the "green" chain helps explain how it would slip in neither direction besides just stating that it's obvious. It seems to me that the chain underneath does nothing as long as you assume that the top part of the chain doesn't move to start off with. You can't just claim that.
RE: RE: Physics Question by CookieRevised on 02-27-2010 at 07:53 PM
quote:You do not add any more mass to one end than on the other end, therefore eventhough the centerpoint might be vertically lower, it stays in the same horizontal position and thus hasn't any influence on where the chain would move.
Originally posted by foaly
quote:
Originally posted by CookieRevised
You simply hang a second chain of the same type as the one you had on both the ends. This does _not_ change anything in the system since the chain would pull equally hard on both sides; aka the two opposite forces (one on the left end, the other on the right end) cancel eachother out. But, it is now a lot easier to see in pic4 why there wouldn't be a movement, not even in a frictionless environment; it's just a closed chain hanging on a irregular object; it is never going to move out of itself.
It would actually, you move the centerpoint of the mass of the chain...
What you say is that if you add 10Kg on both ends the chain would suddenly behave differently than before. This is not the case. The chain will not move any differently than before.
Or to put it in another way, what you say is that a lighter chain is going to behave differently than a heavier chain, eventhough the lay on the exact same triangle in the exact same position. yes, the complete system (chain + block) is going to be heavier, but that does not influence the movement of the chain at all.
If you add 10Kg on both the sides of a scale in balance, that scale isn't going to move, it would stay where it is. If you add 10Kg on both sides in an unbalanced system, that unbalanced system isn't going to flip to one side any faster than it was before or all of a sudden flip to the other side. Aka: adding an equal force to both sides of a balance system (which might be in balance or not, doesn't matter) is not going to have ANY influence at all on the balance of that system.
quote:sorry, I didn't meant "/" as in an divided by symbol. "<=>" or whatever might have been a better symbol; x and y are those formulas provided by Chancer and co above (which I explained in that same post). You can also think of x and y as both ends of a scale and the "/" as the tipping point.
Originally posted by Chrono
quote:1/2 != 11/12
Originally posted by CookieRevised
It's like saying x/y wouldn't be the same as x+10 / y+10.
quote:I didn't ignore anything. In the reply I gave I replied to every bit of your post. See second paragraph (talking about "not possible in real life") and third paragraph (talking about superconductors etc).
Originally posted by vaccination
Why ignore half my post? -.-
quote:No there isn't. You have exactly the same additional force pulling on the right side as you have the same additional mass on the right side! Hence the system does NOT change by adding the bottom chain!
Originally posted by vaccination
quote:
Originally posted by CookieRevised
There is no more (or less) force pulling on the chain on the left side than there is on the right side, ergo, there is nothing to start movement, ergo there is no movement, even in a theoretical frictionless system, no matter what angle or length the two slopes are, as long as both ends are on the same horizontal plane. The system is always in equilibrium.
I'm (almost) sure that if you take those equations from above and work them further out you would see they are equal (you can in theory because there is always a direct relation between the various elements of the two sides (mass, length, angle, etc), by using ratios instead of real numbers)). The more I think about it the more I am convinced of that.
Uhm, yes there is. F = mgh. The force due to gravity is greater on the left side as there is more mass.
quote:Why using 'difficult' equations and 'hard' to understand diagrams when you might solve it with simple logic.
Originally posted by gif83
I already showed this in both my posts. Maybe it's hard for you to understand that without diagrams. The equations do equate.
quote:dunno... because it is obvious* (without the use of equations and too much thinking)?
Originally posted by gif83
I'm still not entirely sure how the "green" chain helps explain how it would slip in neither direction besides just stating that it's obvious.
*A closed chain isn't going to start moving out of itself all of a sudden. reason: see previous posts.
quote:Yes I can claim that. Because if the bottom part isn't going to do anything, as you say, than why should the top part move at all as they are connected... Implying that the top part moves implies automatically that the bottom part would also move, which it does not. And that is the whole essence.
Originally posted by gif83
It seems to me that the chain underneath does nothing as long as you assume that the top part of the chain doesn't move to start off with. You can't just claim that.
RE: Physics Question by gif83 on 02-27-2010 at 08:14 PM
quote:
Originally posted by CookieRevised
Yes I can claim that. Because if the bottom part isn't going to do anything, as you say, than why should the top part move at all as they are connected... Implying that the top part moves implies automatically that the bottom part would also move, which it does not. And that is the whole essence.
What I meant was the bottom chain doesn't move ONLY IF the top doesn't move. you are trying to work out whether or not the top part of the chain moves. You can't say the top does't move because the bottom does as the bottom's movement is dependent on what's going on on top.
I guess I found equations to be far less brain hurt
RE: RE: Physics Question by CookieRevised on 02-27-2010 at 08:25 PM
quote:Since the chains ARE connected you can turn it the other way around too, that is pure logic and exactly the whole essence (and beauty?) of this method.
Originally posted by gif83
What I meant was the bottom chain doesn't move ONLY IF the top doesn't move. you are trying to work out whether or not the top part of the chain moves.
You can't say the top does't move because the bottom does as the bottom's movement is dependent on what's going on on top.
Neither the top or the bottom can move as long as the bottom or the top will not move. No need for equations, diagrams and maths (well except for: If A is B, then B is A).
quote:bleh, as long as we agree the top chain wouldn't move
Originally posted by gif83
I guess I found equations to be far less brain hurt
RE: Physics Question by gif83 on 02-27-2010 at 08:36 PM
quote:
Originally posted by CookieRevised
Neither the top or the bottom can move as long as the bottom or the top will not move. No need for equations, diagrams and maths (well except for: If A is B, then B is A)
Agreed. However, as of such there is nothing so far I have seen that says either side will not move. If you say the top side will not move then the bottom chain is pointless. if you say the bottom chain won't move, how can you say that without knowing about the top?
I'm probably just being really dense here.
RE: Physics Question by foaly on 02-27-2010 at 08:43 PM
quote:
Originally posted by CookieRevised
quote:You do not add any more mass to one end than on the other end, therefore eventhough the centerpoint might be vertically lower, it stays in the same horizontal position and thus hasn't any influence on where the chain would move.
Originally posted by foaly
quote:
Originally posted by CookieRevised
You simply hang a second chain of the same type as the one you had on both the ends. This does _not_ change anything in the system since the chain would pull equally hard on both sides; aka the two opposite forces (one on the left end, the other on the right end) cancel eachother out. But, it is now a lot easier to see in pic4 why there wouldn't be a movement, not even in a frictionless environment; it's just a closed chain hanging on a irregular object; it is never going to move out of itself.
It would actually, you move the centerpoint of the mass of the chain...
What you say is that if you add 10Kg on both ends the chain would suddenly behave differently than before. This is not the case.
That is not what I'm saying at all. Because you lower the balance of the chain way below the tumble point, you make it easier for the chain to balance...
What is probably even more important is that by adding the chain you make a circle, this makes the chain have to pull itself down when sliding one way or another...
I'll add a picture in a sec showing how ludicrous it is that you could just add a chain and expect it to be the same situation....
Without the green chain the chain will obviously fall left, with it, it won't...
Although the blue and red chain aren't on the same horizontal height as the examples you gave... The theory behind it is still the same... You can't just connect the chain... it makes it a totally different object, that behaves completely differently
RE: Physics Question by vaccination on 02-27-2010 at 09:00 PM
Cookie, connecting the chains is NOT the same as adding a 10kg weight to either side. Lets say you connect a 20kg chain to the ends of the other chain (ie: the green chain in your diagrams has a mass of 20kg) this is not evenly distributed to 10kg at each end of the initial chain, like it would if you simply attached a 10kg mass to each end, instead the majority of the 20kg mass of the new chain falls downwards and to the middle, meaning that an extra 20kg of mass is now in effect on the original chain at the point where the two slopes meet.
Anyway, if you can't understand how f= mgh works, I would just stop posting in this thread, since you've mostly posted nonsense, I'm afraid. I mean, three of your four diagrams don't even match the criteria of the experiment(ignoring the absurdity of this random extra chain you've decided to magic up).
RE: RE: Physics Question by CookieRevised on 02-27-2010 at 09:06 PM
quote:Easier or harder is irrelevant. The thing would still be in the exact same state. The center of gravity has got nothing todo in all of this.
Originally posted by foaly
That is not what I'm saying at all. Because you lower the balance of the chain way below the tumble point, you make it easier for the chain to balance...
0.999999999999999999 is still lower than 1. It is not because it is 'closer' to one than 0.5 that it isn't lower anymore.
quote:no. It pulls itself down _equally_ on both side, aka it cancels itself out! It does _not_ pull harder on one side than on the other side; it pulls equally hard on _both_ sides.
Originally posted by foaly
What is probably even more important is that by adding the chain you make a circle, this makes the chain have to pull itself down when sliding one way or another...
quote:Your drawing is a complete different system than what SonicSam has drawn. My drawings in my previous post are of the exact same system as what SonicSam has drawn. Notice that in the system of SonisSam the end points lay on the same horizontal plane.
Originally posted by foaly
I'll add a picture in a sec showing how ludicrous it is that you could just add a chain and expect it to be the same situation....
hence:
quote:But you are using a different system than SonicSam, not me.
Originally posted by foaly
....The theory behind it is still the same...
quote:Sorry, but it certainly is. Look again at SonicSam's drawing...
Originally posted by vaccination
Cookie, connecting the chains is NOT the same as adding a 10kg weight to either side.
quote:Of course it is not 10Kg pulling on either side, but it IS evenly distributed. Hence there is no extra force pulling more on one side than it is on the other! That is basic (vector) math.
Originally posted by vaccination
Lets say you connect a 20kg chain to the ends of the other chain (ie: the green chain in your diagrams has a mass of 20kg) this is not evenly distributed to 10kg at each end of the initial chain
x y
\ /
\ /
|
#20Kg
quote:I'm sorry, but what I posted is 100% correct and I even apply that science in every day work when I need to fly spot lights and scenery in the theater (hence the reason how I came up with that extra chain)
Originally posted by vaccination
...like it would if you simply attached a 10kg mass to each end, instead the majority of the 20kg mass of the new chain falls downwards and to the middle, meaning that an extra 20kg of mass is now in effect on the original chain at the point where the two slopes meet.
Anyway, if you can't understand how f= mgh works, I would just stop posting in this thread, since you've mostly posted nonsense, I'm afraid.
quote:They _all_ match exactly the criteria...
Originally posted by vaccination
I mean, three of your four diagrams don't even match the criteria of the experiment (ignoring the absurdity of this random extra chain you've decided to magic up).
And again, the extra chain does not have _any_ influence on the balance of the system.
RE: Physics Question by foaly on 02-27-2010 at 09:14 PM
quote:
Originally posted by CookieRevised
Easier or harder is irrelevant. The thing would still be in the exact same state. The center of gravity has got nothing todo in all of this.
So if we would double the weight at the left (and only effecting the center of the gravity) it wouldn't change anything?
I'm still not sure if you are serious or are just trying to troll us with your Zeno style logic...
You are right though...:
if (cos A)*(mass of chain above BC) > (cos G)*(mass of chain above AC), it will fall to the left.
if (cos A)*(mass of chain above BC) < (cos G)*(mass of chain above AC), to the right.
lets assume the mass of the chain is equal to the distance...
cos A = CD / BC -> CD = cos A * BC
cos G = CD / AC -> CD = cos G * AC
-->
cos A * BC = cos G * AC
so it will balance...
The way you came to your conclusion just seems wrong
RE: Physics Question by vaccination on 02-27-2010 at 09:23 PM
quote:No, because you are you are adding additional forces in different directions that aren't there in the original system. For example, the horizontal and vertical forces exerted by that chain create two new component forces acting down and towards the centre(which would acts against the slopes).
Originally posted by CookieRevised
Of course it is not 10Kg pulling on either side, but it IS evenly distributed. Hence there is no extra force pulling more on one side than it is on the other! That is basic (vector) math.
x y
\ /
\ /
|
#20Kg
quote:No they don't. The first 3 of your diagrams contain two slopes at the same angle as each other, Sam's criteria is that one be "flatter" (at a smaller angle to the horizontal) than a "steeper" slope (at a greater angle to the horizontal). Maybe *you* should look at it again.
Originally posted by CookieRevised
The _all_ math exactly the criteria...
RE: Physics Question by CookieRevised on 02-27-2010 at 09:24 PM
quote:Do not take my words out of context. Of course it would change if you would add a force only to one side. But you do not put an extra weight on JUST the left side, you also do the exact same thing on the right!!!!!!!
Originally posted by foaly
quote:
Originally posted by CookieRevised
Easier or harder is irrelevant. The thing would still be in the exact same state. The center of gravity has got nothing todo in all of this.
So if we would double the weight at the left (and only effecting the center of the gravity) it wouldn't change anything?
Or: how is connecting a chain to both sides going to pull on one side harder than on the other?? That is completely impossible, the chain will pull on both sides equally hard (which is what I've said 1243123 times before, but blah)
quote:dead serious...
Originally posted by foaly
I'm still not sure if you are serious or are just trying to troll us with your Zeno style logic...
RE: Physics Question by foaly on 02-27-2010 at 09:27 PM
quote:
Originally posted by CookieRevised
quote:Do not take my words out of context. Of course it would change if you would add a force only to one side. But you do not put an extra weight on JUST the left side, you also do the exact same thing on the right!!!!!!!
Originally posted by foaly
quote:
Originally posted by CookieRevised
Easier or harder is irrelevant. The thing would still be in the exact same state. The center of gravity has got nothing todo in all of this.
So if we would double the weight at the left (and only effecting the center of the gravity) it wouldn't change anything?
Or: how is connecting a chain to both sides going to pull on one side harder than on the other?? That is completely impossible, the chain will pull on both sides equally hard (which is what I've said 1243123 times before, but blah)
see the edit of my last post
RE: RE: Physics Question by CookieRevised on 02-27-2010 at 09:32 PM
quote:Forces which cancel eachother out!!!!!!!!
Originally posted by vaccination
No, because you are you are adding additional forces in different directions that aren't there in the original system.
quote:You just proved my point....
Originally posted by vaccination
For example, the horizontal and vertical forces exerted by that chain create two new component forces acting down and towards the centre(which would acts against the slopes).
"acting down and towards the centre"...
aka: they cancel eachother out as they are in opposite direction and there is only a downward net force going from the center of mass strait down. Any extra force going strait down on the center of mass does not have any influence on the movement of that mass, in any system, frictionless, vacuum, whatever. And since the center of mass has therefore NOT moved an inch in the horizontal plane, not a tiny tiny fraction, it is still exactly above the same point as it was before and therefore that extra chain has got NO influence at all on the movement of the top chain.
quote:Sorry, but ever heared of limits and delta values?
Originally posted by vaccination
quote:No they don't. The first 3 of your diagrams contain two slopes at the same angle as each other, Sam's criteria is that one be "flatter" (at a smaller angle to the horizontal) than a "steeper" slope (at a greater angle to the horizontal). Maybe *you* should look at it again.
Originally posted by CookieRevised
They _all_ math exactly the criteria...
State what you want, the picture shows exactly what the limits of the system are and is according every criteria SonicSam's teacher has given.
RE: Physics Question by vaccination on 02-27-2010 at 09:34 PM
quote:delta != the same
Originally posted by CookieRevised
quote:Sorry, but every heared of limits and delta values?
Originally posted by vaccination
quote:No they don't. The first 3 of your diagrams contain two slopes at the same angle as each other, Sam's criteria is that one be "flatter" (at a smaller angle to the horizontal) than a "steeper" slope (at a greater angle to the horizontal). Maybe *you* should look at it again.
Originally posted by CookieRevised
They _all_ math exactly the criteria...
State what you want, the picture shows exactly what the limits of the system are and is according every criteria SonicSam has given.
quote:
Originally posted by CookieRevised
aka: they cancel eachother out as they are in opposite direction and there is only a downward net force going from the center of mass strait down. Any extra force going strait down on the center of mass does not have any influence on the movement of that mass, in any system, frictionless, vacuum, whatever. And since the center of mass has therefore NOT moved an inch in the horizontal plane, not a tiny tiny fraction, it is still exactly above the same point as it was before and therefore that extra chain has got NO influence at all on the movement of the top chain.
Okay now I see what you're saying, but the forces wouldn't be the same either side, surely?
RE: Physics Question by Volv on 02-27-2010 at 09:34 PM
quote:
Originally posted by CookieRevised
Both the ends of the chain must be at the same horizontal plane, see picture from SonicSam.
quote:Mathematically it is true that if both ends of the chain are on the same horizontal plane then there will be no net force, hence no movement.
Originally posted by Volv
If that was a parameter of SonicSam's question then yes, you are absolutely right
Cookie is also correct when he says that a system in which the chain is joined makes no difference to the model whatsoever given that the ends of the sloped surface are on the same horizontal plane -- and as there is no net force to start with (whether the chain is joined or not) then there will be no movement.
If they were not on the same horizontal plane then yes, there may be a net force on an un-joined chain. However, if the chain is joined then unlike the previous example, there is not an even distribution of the hanging chain between the two sides (since the surface is not on the same horizontal plane, there will be more hanging from the shorter side), this uneven distribution acts to negate any net force which may have existed in an unconnected chain and as such there will still be no movement in a circular chain.
RE: Physics Question by billyy on 02-27-2010 at 09:58 PM
Are you saying that when the surfaces end at the same height the angle of the first slope will allways cancell out the size of the chain on the second slope?
So none of these would move?
![[Image: nomoveg.png]](http://img714.imageshack.us/img714/1193/nomoveg.png)
Because that was whut i was thinking...
however i think the green chain doesn't prove anything, using that no chain would ever move... so in this case it doesn't change anything but it doesn't prove anything either 
RE: Physics Question by Volv on 02-27-2010 at 10:15 PM
quote:That's what the maths says
Originally posted by billyy
Are you saying that when the surfaces end at the same height the angle of the first slope will allways cancell out the size of the chain on the second slope?
So none of these would move?
Because that was whut i was thinking...
quote:Yep, a round chain wouldn't move in any situation. However when the surfaces end at the same height then there's no net force on the green part below, therefore if there's a net force on the red (top) part, then it would cause it to move. Given that, and since we know the linked chain won't move on its own there must therefore be no net force on the top (red) part.
Originally posted by billyy
however i think the green chain doesn't prove anything, using that no chain would ever move... so in this case it doesn't change anything but it doesn't prove anything either
I think that's what Cookie is trying to say anyway.
RE: Physics Question by CookieRevised on 02-27-2010 at 10:20 PM
quote:
Originally posted by Volv
quote:Yep, a round chain wouldn't move in any situation. However when the surfaces end at the same height then there's no net force on the green part below, therefore if there's a net force on the red (top) part, then it would cause it to move. Given that, and since we know the linked chain won't move on it's own there must therefore be no net force on the top (red) part.
Originally posted by billyy
however i think the green chain doesn't prove anything, using that no chain would ever move... so in this case it doesn't change anything but it doesn't prove anything either
I think that's what Cookie is trying to say, and it's true.
exactly... and no maths or equations involved here...
PS: will you be my personal thought translator? I'll even pay you
PS: what Volv said is almost exactly the same as what I've said the first time though... but oh well...
quote:
Originally posted by Volv
Yep, a round chain wouldn't move in any situation. However when the surfaces end at the same height then there's no net force on the green part below, therefore if there's a net force on the red (top) part, then it would cause it to move. Given that, and since we know the linked chain won't move on its own there must therefore be no net force on the top (red) part.
I think that's what Cookie is trying to say anyway, and it's true.
quote:
Originally posted by CookieRevised before people started to question each word
Think about it, what if you have something hanging from below connecting both ends of the chain. It would mean that there would be a 'force' pulling on each side equally from below no (so it doesn't matter if it is there or not)? So, if the top piece of the chain would move to some direction, it means the bottom part would move too (in the opposite direction). If that would happen, you would have a perpetual machine! Which isn't possible... hence, it would never move, no matter the angles and the lengths of the slopes, as long as both the 'bottom' parts are on a horizontal plane.
RE: Physics Question by gif83 on 02-27-2010 at 10:59 PM
quote:
Originally posted by Volv
quote:That's what the maths says
Originally posted by billyy
Are you saying that when the surfaces end at the same height the angle of the first slope will allways cancell out the size of the chain on the second slope?
So none of these would move?
Because that was whut i was thinking...
quote:Yep, a round chain wouldn't move in any situation. However when the surfaces end at the same height then there's no net force on the green part below, therefore if there's a net force on the red (top) part, then it would cause it to move. Given that, and since we know the linked chain won't move on its own there must therefore be no net force on the top (red) part.
Originally posted by billyy
however i think the green chain doesn't prove anything, using that no chain would ever move... so in this case it doesn't change anything but it doesn't prove anything either
I think that's what Cookie is trying to say anyway.
Thanks for the translation Volv. That was turning my brain to mush.